다중공산성과 분산팽창계수
다중공산성은 주관심대상인 종속변수 Y에 대해 설명하려는 독립변수들 간
강한 상관관계로부터 나온다.
다중공산성은 회귀분석 모델링을 할 때 다양한 이유로 분석가들을 괴롭히는
문제이다.
따라서 다중공산성 문제를 사전에 방지하기 위해 다양한 진단법이
존재한다.
그중 하나가 분산팽창계수를 계산하여 분산팽창요인 여부를 찾는 방법이
있다.
분산팽창요인(Variance Inflation Factor) 줄여서 VIF는 다음과 같이 찾을 수 있다.
우선 다중회귀분석 시 종속변수 Y를 제외하고
나머지 독립변수간의 상관관계만을 고려하여 2개 이상의 독립변수 조합 간
회귀분석을 따로 실시한다.
실시해본 결과 설명력(결정계수 ; R2)이 높으면 우리가
우려하는 다중공산성문제가 발생되는 것이며
만약 독립변수 간 상관관계가 높아 특정조합상(i 번째 독립변수를 종속변수로
두어 회귀분석 실시)에서 회귀선의 설명력이 좋으면 분산팽창계수 값이
커지게 된다.
분산팽창계수의 정의는 아래와 같다.
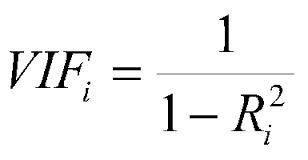
보통 이 분산팽창계수가 10 이상일때 j번째 독립변수는 다중공산성이 있는 독립변수라 판단한다.
Boston 데이터셋을 이용한 실습예제
Boston 데이터셋을 이용하여 다중공산성이 있는 독립변수가 존재하는지
R에서 vif() 함수를 이용하여 찾아보겠다.
우선 vif() 는 car package 안에 내장되어있는
함수이다.
필요에 따라 패키지를 설치하고 로드한다.
install.packages("car")
library("car")MASS package 에 있는 Boston 데이터셋을 이용할 수 있도록
준비한다.
참고로 Boston 데이터는 집값에 영향을 주는 것으로 생각되는 요인들을
정하여 Boston 지역 부근의 집들을 전수조사한 데이터라고 한다.
data(Boston, package = "MASS")
summary(Boston)## crim zn indus chas
## Min. : 0.00632 Min. : 0.00 Min. : 0.46 Min. :0.00000
## 1st Qu.: 0.08204 1st Qu.: 0.00 1st Qu.: 5.19 1st Qu.:0.00000
## Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.00000
## Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.06917
## 3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.00000
## Max. :88.97620 Max. :100.00 Max. :27.74 Max. :1.00000
## nox rm age dis
## Min. :0.3850 Min. :3.561 Min. : 2.90 Min. : 1.130
## 1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100
## Median :0.5380 Median :6.208 Median : 77.50 Median : 3.207
## Mean :0.5547 Mean :6.285 Mean : 68.57 Mean : 3.795
## 3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188
## Max. :0.8710 Max. :8.780 Max. :100.00 Max. :12.127
## rad tax ptratio black
## Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
## 1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38
## Median : 5.000 Median :330.0 Median :19.05 Median :391.44
## Mean : 9.549 Mean :408.2 Mean :18.46 Mean :356.67
## 3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23
## Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
## lstat medv
## Min. : 1.73 Min. : 5.00
## 1st Qu.: 6.95 1st Qu.:17.02
## Median :11.36 Median :21.20
## Mean :12.65 Mean :22.53
## 3rd Qu.:16.95 3rd Qu.:25.00
## Max. :37.97 Max. :50.00종속변수는 집값을 의미하는 medv 변수로 할 것이다.
나머지 변수 중 이산형 자료로 판단되는 chas,
rad 변수는 편의상 제외하고 독립변수로 설정해 다중회귀적합을
해본 결과이다.
str(Boston) # chas, rad 변수가 integer type 인 것을 확인할 수 있음## 'data.frame': 506 obs. of 14 variables:
## $ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
## $ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
## $ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
## $ chas : int 0 0 0 0 0 0 0 0 0 0 ...
## $ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
## $ rm : num 6.58 6.42 7.18 7 7.15 ...
## $ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
## $ dis : num 4.09 4.97 4.97 6.06 6.06 ...
## $ rad : int 1 2 2 3 3 3 5 5 5 5 ...
## $ tax : num 296 242 242 222 222 222 311 311 311 311 ...
## $ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
## $ black : num 397 397 393 395 397 ...
## $ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
## $ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...data <- subset(Boston, select = -c(chas, rad)) # integer type 인 chas, rad 변수 독립변수에서 제외
lmfit <- lm(medv ~ . , data = data)
summary(lmfit)##
## Call:
## lm(formula = medv ~ ., data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.3315 -2.8771 -0.6792 1.6858 27.4744
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.970e+01 5.051e+00 5.879 7.59e-09 ***
## crim -7.010e-02 3.269e-02 -2.144 0.032482 *
## zn 3.989e-02 1.409e-02 2.831 0.004835 **
## indus -4.198e-02 6.080e-02 -0.691 0.490195
## nox -1.458e+01 3.899e+00 -3.740 0.000206 ***
## rm 4.188e+00 4.255e-01 9.843 < 2e-16 ***
## age -1.868e-03 1.359e-02 -0.137 0.890696
## dis -1.503e+00 2.059e-01 -7.301 1.15e-12 ***
## tax 8.334e-04 2.386e-03 0.349 0.727038
## ptratio -8.738e-01 1.323e-01 -6.607 1.02e-10 ***
## black 8.843e-03 2.763e-03 3.200 0.001461 **
## lstat -5.267e-01 5.224e-02 -10.083 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.899 on 494 degrees of freedom
## Multiple R-squared: 0.7225, Adjusted R-squared: 0.7163
## F-statistic: 116.9 on 11 and 494 DF, p-value: < 2.2e-16다중회귀분석 결과를 summary() 함수로 간단히
살펴보면
독립변수 각각에 대한 회귀계수들과 유의성을 판단할 수 있는 output 들이
출력 된다.
하지만 지금까지 나와 있는 output 만을 보고 다중공산성이 있는지 없는지
판단하기는 쉽지 않다.
vif() 함수를 꺼내 들어보겠다.
vif() 함수 사용방법은 아주아주 간단한 편이다. 아래코드처럼
lm() 함수로 반환된 객체를 넣어주기만 하면 된다.
vif(lmfit)## crim zn indus nox rm age dis tax
## 1.663648 2.272992 3.660714 4.294324 1.880883 3.077311 3.953729 3.403205
## ptratio black lstat
## 1.725085 1.338875 2.928554vif(lmfit) > 10## crim zn indus nox rm age dis tax ptratio
## FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## black lstat
## FALSE FALSEvif() 함수를 실행해 본 결과 종속변수를 제외한 독립변수가
나열되고, 그 밑에 각 독립변수의 분산팽창계수값이 출력된다.
값을 보니 10을 넘는 변수가 존재하지 않다.
따라서 현 분석에서 다중공산성이 존재하는 독립변수는 없다고 결론을 낼 수
있겠다.