수학공부 중 종종 이런일이 많았다.
원 공식에 의해 계산이 불가하거나 손으로 풀기 복잡할 경우 근사치에
대한 간편공식을 배우게 되는 경우가 있다.
그 간편공식으로써 풀은 결과물이 원 공식으로 풀은 결과물과 동일한지
비교해보는 작업을 R을 이용하여 자주 하곤 했다.
만약 그 결과물이 어떤 하나의 스칼라값으로 나온다면,
금방 비교하여 동일한지 여부를 파악할 수 있다.
R을 이용한다면 논리연산자를 이용해 빠르고 정확하게 비교가 가능할
것이다.
== 의 기호는 데이터셋의 원소별로 동일하면 TRUE, 틀리면
FALSE 를 반환하게 되므로 좌변과 우변이 같은지를 아래처럼 확인할 수
있다.
2/3 == 804/1206## [1] TRUE위의 예시처럼 쉽게 같은지 구분하기 힘든것을 논리연산자를 통해 동일한지 파악할 수 있다.
all.equal() 함수
그런데 이러한 논리연산자 말고, R에서는 오늘 알아볼
all.equal() 이란 함수가 있다.
이 함수의 쓰임은 비교하고자 하는 2개의 R객체가 동일한지를 확인1해 준다.
가끔, 아니 곧잘 대용량의 크기가 큰 데이터셋의 동일여부를 파악해야 할
때도 있을것이다.
아래와 같은 상황을 예로 들어 보겠다.
## 일반 행렬곱셈
A <- matrix(round(rnorm(600 * 400)), nrow = 600, ncol = 400)
B <- matrix(round(rnorm(400 * 800)), nrow = 400, ncol = 800)
AB <- A %*% B
## 분할행렬 생성
A11 <- A[1:200, 1:200]
A12 <- A[1:200, 201:400]
A21 <- A[201:600, 1:200]
A22 <- A[201:600, 201:400]
B11 <- B[1:200, 1:200]
B12 <- B[1:200, 201:800]
B21 <- B[201:400, 1:200]
B22 <- B[201:400, 201:800]
partition_AB <- rbind(
cbind(A11 %*% B11 + A12 %*% B21, A11 %*% B12 + A12 %*% B22),
cbind(A21 %*% B11 + A22 %*% B21, A21 %*% B12 + A22 %*% B22)
) # 분할행렬 생성 후 행렬곱셈위의 코드가 무엇인지 간략하게 설명하면
첫번째는 임의의 행렬 A와 행렬 B를 생성시킨 후,
두 행렬의 곱셈을 AB로 할당한 것이며,
두번째는 행렬 A, B 를 이와 같이 알맞게 분할한
후
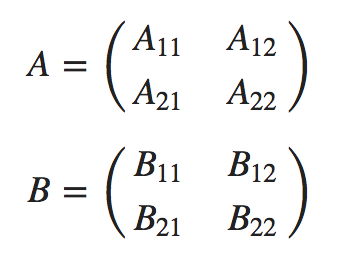
단 A11, B11 은 200×200 행렬
로 분할한 행렬을 이용하여 행렬 A, B를 곱한
것 이다.
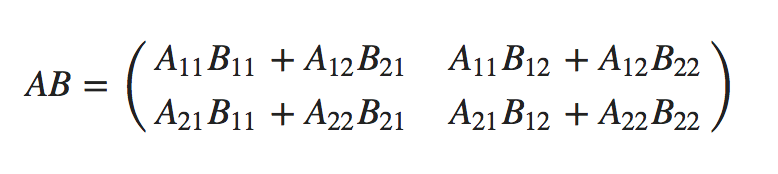
이처럼 곱한것을 객체 partition_AB로 할당하였다.
이론적으로는 첫번째 일반적인 곱셈과, 두번째 분할행렬을 이용한 곱셈과
값이 동일하다.
단 그것이 믿겨지지 않을 경우 직접 확인해 보고싶을 수 있다.
그런데 이때 애로사항이 있다.
AB 와 partition_AB 가 서로 동일하느냐 를
확인하기 위해선
두 행렬의 사이즈가 600×800 으로 매우 부담이 되는 크기이다.
물론 논리연산자 == 를 써도 되겠지만, 문제는 이 논리연산자를 써서 아래 코드를 실행하게 될 경우
AB == partition_AB행렬의 원소별 값이 동일한지에 대한 논리값을 600 × 800 = 480,000 개를
행렬 타입으로 거대하게 반환할 것이다. 거대하므로 눈으로 동일한지 확인이
어려울 것이다.
480,000개의 원소가 모두 TRUE 인지를 확인하기 위해
all(AB == partition_AB)## [1] TRUE처럼 all() 함수의 도움을 받을 수도 있겠지만
all.equal() 함수를 사용하는것이 더 유용할 때가 있다.
all.equal(AB, partition_AB)## [1] TRUE함수이름 그대로 all equal 하면 TRUE
그렇지 않을 경우 어디가 어떻게 틀린지 구체적으로 설명한다.
본 예제의 경우 원래의 행렬곱과 분할행렬의 곱이 같은경우의 예제이므로
TRUE 를 반환한다.
all.equal() 함수는 객체가 동일한지의 판단하는 함수로써도
편리한 기능의 함수이지만,
기본적으로는 얼마나 가깝게 동일한지 정도를 확인할 수 있는 일종의
비교함수로 보고 사용하는것이 좋다.
함수 도움말의 제목에서도 ‘Test if Two Objects are (Nearly) Equal’ 로
나와있고 괄호의 “Nearly” 가 눈에 띈다.
조금 더 체감하기 좋은 행렬의 연산예시를 들어보겠다.
R에서는 순환소수, 무한소수를 계산할 때, 즉 유리수가 아닌 무리수를 연산할
때 아주 미세한 값의 차이가 존재할 수 있다.2
하지만 이는 무리수를 굳이 소수점으로 표현하여 어떤 소수점자리 이후는
절단되어 버려지는 시스템 적인 문제일 뿐이다.
아래 예시는 임의행렬 X와 그의 역행렬을 곱한것을 단위행렬과 비교해본
시뮬레이션이다.
행렬 X는 5×5 행렬이며 이론상으로는
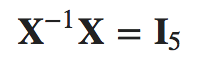
이 성립한다. 하지만
X <- matrix(rnorm(25), 5, 5)
XtX <- solve(X) %*% X
I_5 <- diag(1, 5)
XtX == I_5## [,1] [,2] [,3] [,4] [,5]
## [1,] FALSE FALSE FALSE FALSE FALSE
## [2,] FALSE FALSE FALSE FALSE FALSE
## [3,] FALSE FALSE FALSE TRUE FALSE
## [4,] FALSE FALSE FALSE TRUE TRUE
## [5,] FALSE FALSE FALSE FALSE FALSE결과는 여기저기서 FALSE 가 있고 실제로 값이 다르다. 전부
TRUE 이어야 하지만
table(XtX == I_5)##
## FALSE TRUE
## 22 3이처럼 3개만 TRUE 로 인식한다.
이처럼 무리수를 컴퓨터가 정확하게 표현할 수 없기 때문에 일어나는 일로
XtX 나, I_5 를 같지 않다고 판단하는것은 상황에
따라서 용인해야할 때가 있다.
이때 방금 언급한 all.equal() 함수를 사용해 보면 어떨까?
all.equal(XtX, I_5)## [1] TRUEall.equal() 함수 내에는 tolerance 인자가
존재하여 어느 정도의 차이는 단어 뜻대로 관용, 아량을 베풀어주는 로직이
있다.
따라서 XtX 와, I_5 는 그정도 차이는 무시하고
서로 동일하다고 판단하여 TRUE 를 반환한다.
만약 관용, 아량을 전혀 베풀지 않는(tolerance = 0)다면
all.equal(XtX, I_5, tolerance = 0)## [1] "Mean relative difference: 2.806783e-15"두 객체간 차이의 아주 정확한 값을 반환한다.
분석을 하다보면 위의 예제 말고도 동등성을 확인하여야 할 때가 사뭇
많다.
이럴 때 all.equal() 함수는 유용하게 사용될 수
있을것이다.