통계 비전공자에게 중심극한의 정리를 설명해야 했던 적이
있었는데,
심오한 이론들을 증명하며 설명하느니 한번 보여주는 것이 더 큰 공감을
얻게될 것 같아 animation plot 을 준비한적이 있다.
본 포스팅 글은 R markdown 포맷에서 코드청크옵션
fig.show = "animate" 을 통해 animation plot 을 준비하는
것이 가능하다는 것을 소개하고 그 예시로 중심극한정리 시뮬레이션을 통해
설명할 것이다.
중심극한정리 (Central Limit Theorem) 에 대해서
중심극한정리는 표본의 크기가 커짐에 따라 표본평균의 분포가 점점
정규분포로 닮아(근사) 짐을 의미하는 이론이다.
그리고 표본은 어떠한 분포 타입에 나온 것이더라 하더라도 상관없이
중심극한정리에 해당되는것을 특징으로 한다.
여기서 헷갈리는 것이 있을 수 있는데, 표본평균은 단하나의 값으로 분포가
될 수 있느냐 라는 질문이 생길 수 있다.
이 궁금증은 표본 자체가 확률변수라는 것으로써 이해할 수 있다.
표본 자체가 확률변수이므로 이를 종합하여 평균한 값 하나일지라도 분명
확률변수이며 이는 분포로써 설명이 가능하다.
하지만 시뮬레이션에서 사용할 표본평균은 단 한 개 가지고는 분포를
시각적으로 볼 수 없는 노릇이다.
따라서 표본평균들을 여러 개 발생시킬 것이다.
정리하면 시뮬레이션 시 특정 분포에 대해 많은 표본을 뽑은 후
표본평균계산 후 이를 반복해서 다양한 표본평균들을 준비해 히스토그램으로
분포를 확인할 것이다.
또한 표본의 크기가 커짐에 따라 정규분포로 닮아진다는 것을 점근적으로
보여주는 것이 시뮬레이션의 큰 의미라고 볼 수 있다.
우선 현 시뮬레이션에선
- 특정분포를 포아송분포 X ∼ Poisson(λ=10) 으로
- 표본개수는 n=500 으로 통일하고
- 표본평균들을 1,000개 준비하기 위해 위 과정을 1000번 반복
할 것이다.
단편 시뮬레이션
위에서 설명한 시뮬레이션은 아래코드를 통해 확인 가능하다.
res <- replicate(1000, expr={
n <- 500
sample <- rpois(n, lambda = 10)
mean(sample)
})위 코드를 통해 1000개의 표본평균들이 res 객체에
담겨있게된다.
정규분포로 근사되었는지 분포를 확인하는건 2가지 방법을 통해 해보고자
한다.
- 히스토그램과 밀도추정선을 덧그린 plot
- Quantile-Quantile Plots
hist(res, freq = F)
lines(density(res), lty = 2, col = "blue")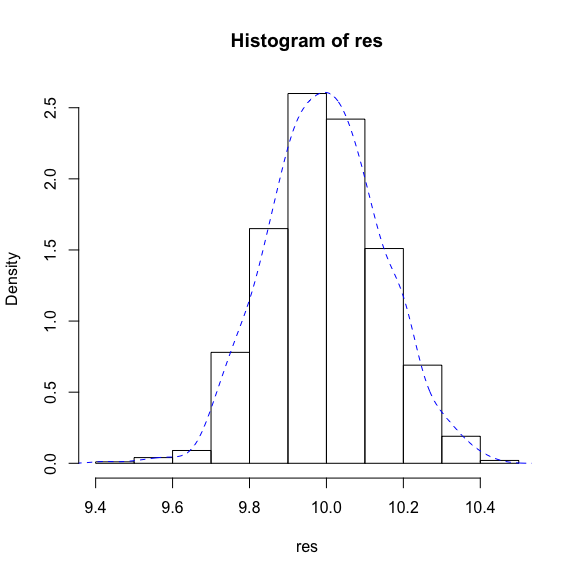
1번에 해당되는 히스토그램이다.
qqnorm(res)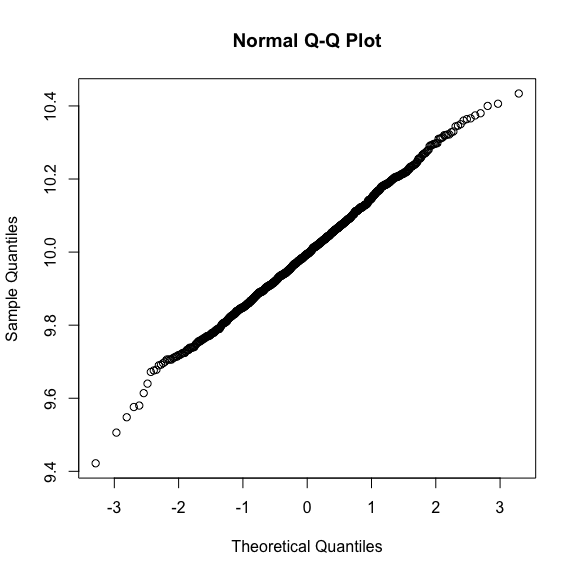
2번에 해당하는 소위 QQplot 이다.
분명 결과물을 통해선 포아송분포에서 뽑은 표본들의 평균의 분포가
정규분포에 근사하는 것을 체감할 수는 있다.
하지만 나는 이것보다 분포의 개수가 많으면 많아질수록 정규분포의 닮아짐이
높아진다는 점근적근사를 시각적으로 보여주고 싶은 것이었다.
Rmarkdown
의 코드청크옵션 fig.show = "animate" 에 대해서
필자는 Rmarkdown 포맷을 자주 사용하여 내 지식을 전달하는 편인데
데이터분석과 융화된 글을 쓰기에 거리낌 없는 도구로 굉장한 공감을 얻었기
때문이다.
특히 fig.show = "animate" 와 같은 코드청크 옵션은 데이터의
변질에 따른 plot output 의 변화를 보여주기에 간편한 기능을 제공해서
적극적으로 애용 중이다.
위의 예시를 이어서 설명하자면 단편적인 시뮬레이션을 통해 정규분포에
근사하는 것을 체감시켰지만,
이보다 더 중요한 것을 설명하기 위해 표본개수 즉 표본평균을 계산한
반복회수가 증가함으로써 일어나는 정규근사 정도를 animation plotting 통해
보여줄 것이다.
아래처럼 말이다.
library(numbers) # for fibonacci function
ani_N <- c()
for(i in 5:30) ani_N[i-4] <- fibonacci(i)
ani_N## [1] 5 8 13 21 34 55 89 144 233 377
## [11] 610 987 1597 2584 4181 6765 10946 17711 28657 46368
## [21] 75025 121393 196418 317811 514229 832040for(N in ani_N){
res <- replicate(N, expr={
n <- 500
sample <- rpois(n, lambda = 10)
mean(sample)
})
hist(res, freq = F, ylim = c(0, 7), xlim = c(9, 11))
lines(density(res), lty = 2, col = "blue")
}for(N in ani_N){
res <- replicate(N, expr={
n <- 500
sample <- rpois(n, lambda = 10)
mean(sample)
})
qqnorm(res, xlim = c(-4, 4), ylim = c(9, 11))
}위의 B장에서 수행했던 코드의 본체는 부수적인 차이만 존재할 뿐 거의
흡사하다.
차이점은 시뮬레이션 본체코드를 for 문을 통해 ani_N 의
피보나치수열로 반복회수를 조정한것이며,
시각화 코드인 hist(), qqnorm() 함수에
xlim, ylim 인자값들을 부여해 범위를
고정시켰다는 차이가 있다.
그리고 본장에서 설명하고자 하는 차이점은 사실 R코드가 아닌 Rmarkdown
코드청크옵션에 내막이 있다.
verbatim 모드로 Rmarkdown 코드청크 전체를 보여주면 아래와 같다.
# ```{r fig.show = "animate", interval = .4}
# for(N in ani_N){
# res <- replicate(N, expr={
# n <- 500
# sample <- rpois(n, lambda = 10)
# mean(sample)
# })
# hist(res, freq = F, ylim = c(0, 7), xlim = c(9, 11))
# lines(density(res), lty=2, col="blue")
# }
# ```사실 코드청크에 fig.show = "animate", interval = .4 와
같은 옵션이 존재하지 않는다면
ani_N 의 마지막 값에 대한 중심극한 시뮬레이션 histogram
결과만 나올것이다.
실제 수행된 코드는 ani_N 에 담겨있는 수열들의 값대로
히스토그램을 그리겠지만 결국 출력되는건 마지막 값에 해당되는 단편
시뮬레이션 plot output 이다.
하지만 코드청크에 fig.show = "animate" 를 부여하면
중간중간에 출력되는 plot output 을 임시로 모두 저장하게된다.
이후 코드청크의 interval 옵션값만큼의 간격으로 저장된 plot
output 프레임들을 순차적으로 인코딩하여 영상을 만든다!
지금은 interval 값을 0.4초로 지정했는데 프레임 넘김을 더 빠르게 하고싶은
경우 이값을 작게 조정하여 희망하는 속도로 맞출 수 있다.
그리하여 피보나치수열 대로 표본이 증가하면 증가할수록 정규분포로
근사되는것을 시각적으로 볼 수 있게 되는 것이다.
QQplot animation 도 마찬가지 형태이다.
# ```{r fig.show = "animate", interval = .4}
# for(N in ani_N){
# res <- replicate(N, expr={
# n <- 500
# sample <- rpois(n, lambda = 10)
# mean(sample)
# })
# qqnorm(res, xlim = c(-4, 4), ylim = c(9, 11))
# }
# ```요구사항
단 이렇게 영상으로 인코딩하는 작업을 하기 위해서 운영체계별로
요구하는 플러그인이 다를 수 있다.
필자는 OSX 에서 이 글을 작성한 것이며 ffmpeg 설치가 요구되었었다.
그리고 이것이 요구사항일지는 모르겠지만 코드수행시간이란 비용 이외에
animation plot 영상을 인코딩하는 시간 역시 필요하다.
위의 예제처럼 간단한 수준의 짧은 영상을 만드는 것은 인코딩시간이 조금
걸리지만,
그렇지 않으면 많은 인내심이 요구될 수 있다.