약 5년전 컨설팅 인턴 일을 하면서 자료포락분석1(Data envelopment analysis 이하
DEA)이 필요했던 시점이 있다.
그때 당시 실제로 분석을 하기 위하여 컴퓨터 프로그램을 이용할 필요가
있었고
Export choice
프로그램을 이용해 DEA 분석을 한 논문들을 상당수 찾을 수 있었다.
하지만 Export choice 는 상용 프로그램이었고 새로 알아야 된다는 점들
때문에 빠르게 시도해 볼 수 없었다.
이때는 깊은 분석보단 만만하게 시도해 볼 수 있었던 환경이
필요했었는데
마침 DEA 를 해볼 수 있는 R package 가 있었고 그 패키지 이름은
Benchmarking 이다.
install.packages("Benchmarking")
library(Benchmarking)Benchmarking 패키지의 dea() 함수를 이용하여 얼마든지
벤치마킹의 대상이 되는 의사결정단위(자료포괄분석에서 이를 Decision
Making Unit. DMU로 줄여 표현한다) 별 efficiencies 값들을 구해낼 수
있었다.
우선 투입요소와 산출요소가 정해지고 그에 따른 정량적인 데이터가
존재하면
각 DMU 에 대한 효율성 평가를 수행할 수 있다.
예제 데이터에 대한 설명
Benchmarking package 안에 있는 데이터 셋 중 하나인
charnes1981 을 예제로 DEA를 간단히 수행해 보겠다.
set.seed(1004)
library(dplyr)
data(charnes1981)
charnes1981 <- charnes1981 %>%
tbl_df %>%
sample_n(20)
charnes1981## # A tibble: 20 x 11
## firm x1 x2 x3 x4 x5 y1 y2 y3 pft
## <int> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <int>
## 1 20 25.42 9.05 29.69 31.74 4 29.43 42.63 23.34 1
## 2 17 22.63 4.43 15.40 15.00 2 17.25 20.80 12.07 1
## 3 53 16.20 7.02 26.94 26.30 9 18.23 22.05 17.56 0
## 4 66 23.32 7.10 24.96 28.56 22 16.81 19.72 18.70 0
## 5 29 10.62 2.55 10.10 9.09 4 6.51 7.02 6.16 1
## 6 60 16.28 4.81 18.20 18.98 5 15.15 18.04 13.58 0
## 7 32 6.30 1.93 7.11 7.68 4 4.59 6.16 4.99 1
## 8 24 19.74 6.43 24.20 25.66 3 25.72 30.81 16.54 1
## 9 64 28.38 8.91 30.95 33.33 8 18.63 24.48 23.13 0
## 10 27 27.20 9.38 37.80 31.55 4 31.31 38.32 25.03 1
## 11 15 4.29 5.42 21.45 17.27 5 14.39 18.30 14.33 1
## 12 22 16.34 5.84 20.89 22.10 4 19.40 25.18 16.52 1
## 13 5 11.62 2.21 6.85 6.37 4 7.81 6.94 5.37 1
## 14 9 34.40 11.04 38.16 42.40 8 26.13 29.80 26.29 1
## 15 45 8.32 3.64 12.92 13.13 2 9.47 11.92 8.85 1
## 16 2 29.26 10.24 41.96 40.65 5 24.69 33.89 26.02 1
## 17 11 52.92 11.67 39.48 39.64 5 39.80 37.73 30.29 1
## 18 49 7.14 5.29 23.10 19.06 8 12.17 16.03 15.82 1
## 19 51 11.88 3.59 13.41 13.82 8 9.96 14.34 9.33 0
## 20 54 82.45 15.52 45.00 44.23 13 59.63 64.41 35.89 0
## # ... with 1 more variables: name <fctr>data 를 불러온 후
설명의 편의상 tibble type 으로 charnes1981 형을 변환 및
20개의 샘플링을 하였다. 2
각 변수들에 대한 설명은 다음과 같다.
firm: 학교별 IDname: 주소x1: education level of the mother
x2: highest occupation of a family member
x3: parental visits to school
x4: time spent with children in school-related topics
x5: the number of teachers at the sitey1: reading score
y2: math score
y3: self–esteem score
x로 시작하는 변수들은 각 학교들에 대한 독립변수(투입요소) 로 볼 수
있고
y로 시작하는 변수들은 그 학교에 대한 평가이므로 종속변수(산출요소) 로 볼
수 있다.
DEA 분석
X <- charnes1981 %>%
select(starts_with("x")) %>%
as.matrix
Y <- charnes1981 %>%
select(starts_with("y")) %>%
as.matrix
dea_res <- dea(X, Y)dea() 함수의
첫번째 인자에는 투입변수에 대한 데이터를 matrix 형으로 입력한다.
위의 예제 경우 5개의 투입변수가 존재하므로 X 처럼 적절하게
묶어주었다.
두번째 인자에는 산출변수에 대한 데이터를 역시 matrix 형으로
입력한다.
마찬가지로 3개의 산출변수를 적절히 묶은 Y 를 입력했다.
dea() 함수로 반환되는 결과물들은 다양하다.
관심대상이 효율성 점수만이라면 아래처럼 eff 속성값만을
호출해 본다.
dea_res$eff## [1] 1.0000000 1.0000000 0.8844074 0.9541975 0.9326048 0.9964845 1.0000000
## [8] 1.0000000 0.9804835 1.0000000 1.0000000 1.0000000 1.0000000 0.9850544
## [15] 1.0000000 1.0000000 1.0000000 1.0000000 0.9713179 1.0000000의사결정단위 70개 별 Efficiencies 값이 출력된다.
학교주소별 Efficiencies 값을 매치시켜 표현해보거나
data.frame(School_site_name = charnes1981$name, Efficiencies = dea_res$eff)## School_site_name Efficiencies
## 1 Racine 1.0000000
## 2 New York 1.0000000
## 3 Fresno 0.8844074
## 4 Jacksonville 0.9541975
## 5 Chigago 0.9326048
## 6 Philidelphia 0.9964845
## 7 Jacksonville 1.0000000
## 8 Portageville 1.0000000
## 9 Flint 0.9804835
## 10 Meridian 1.0000000
## 11 Fall River 1.0000000
## 12 New York 1.0000000
## 13 Lebanon 1.0000000
## 14 Lakewood 0.9850544
## 15 New York 1.0000000
## 16 Buffalo 1.0000000
## 17 Wichita 1.0000000
## 18 San Jose 1.0000000
## 19 Buffalo 0.9713179
## 20 Lebanon 1.0000000아래 plotting 결과물 처럼
제공되는 dea.plot.frontier() 함수 결과물인 효율최적선을
통해
상대적인 효율성 평가를 하는데 용이할 것이다.
dea.plot.frontier(X, Y, txt = T)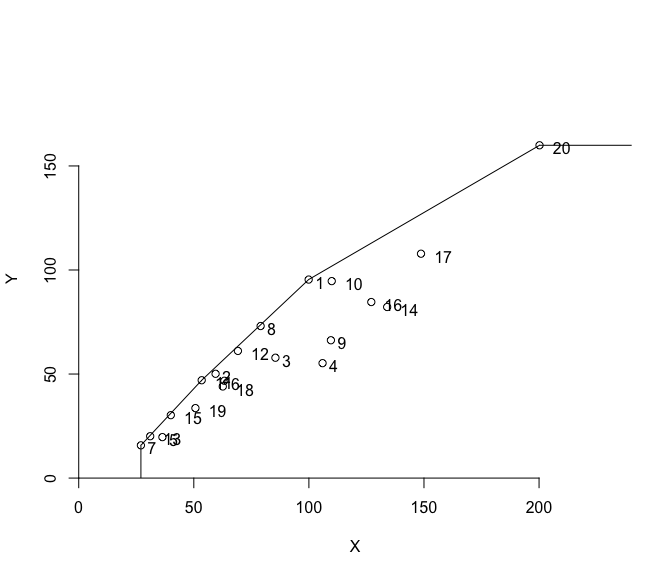
dea() 함수는 DEA분석 주제에 대한 대부분의 기능을
총괄하고 있기 때문에 복잡하고, 제공되는 인자들도 많다.
투입 혹은 산출 관점에 따라 분석방법이 달라지기도 하고,
가정이 달라지기도 한다.
위의 예제처럼 인자의 조종 없이 dea() 함수를 이용하면 기본값
설정을 따르는데
투입기준의 Variable returns to scale 가정을 기반하에 효율성 평가를 한다.
(자세한건 RTS, ORIENTATION 인자의 도움말을
살펴본다)
분석 결과 해석
Efficiency 값이 1인 학교는 투입대비 산출 즉 효율성이 20개의 DMU 와
상대적으로 비교했을 때 가장 높다고 할 수 있다.
하지만 이는 절대적인 효율성 평가가 아닌 상대적 효율성 평가라는 것을 항상
염두해야 한다.
Efficiency 값이 1 미만인 학교는
1의 값을 가진 학교보다 비효율이 발생하고 있다는것을 의미하며
그 값이 작으면 작을수록 비효율이 크다고 해석은 가능하다.