통계학과 대학원 수업 때 미분가능한 연속 함수에 대해서 해를 찾는
방법들을 공부한 적이 있다.
해를 찾아가는 과정들이 알고리즘 방법별로 특색이 있었는데, 원리를
알아가면 알아갈 수록 재미있기도 한 부분이었다.
특히 통계학 수업에선 1학년 학부때 부터 MLE(Maximum Likelihood Estimator)
라는 추정량의 특성을 중요하게 살펴본다.
극대값을 알아내기 위하여 1차 도함수에 해를 찾아내기 위한 훈련을 하면서도
나는 과연 이를 실전에 어떻게 적용할 것인가의 고민을 병행했고,
결과론적으로 프로그래밍을 어떻게 해야하는지 추가적인 고민을 더했던 때가
기억이 난다.
학생을 벗어나 지금은 빅데이터 프로젝트에서 언제한번 이런 해를 찾는
과제를 수행해 볼지 살짝 의문이 들기는 한다.
하지만 빅데이터 프로젝트의 최종 목적지 앞 팔부능선 쯤에는 최적화 문제를
직면하는 분들도 보였고,
서비스가 안정화 되는 시점에서 모델과 추가 실데이터에 대한 2차 타당성
검증이 필요 할 때 역시 최적화가 잘 되었는지의 확인하는 문제로 수렴한다는
생각이 문득 든다.
이런 근사해를 찾는 이론을 바탕으로 근간한 아이디어를 최적화 관점에서
언제 어디선가 써먹을 일이 있지 않을까 싶다.
그런 의미로 대학원 때 배운 Newton Raphson Method 의 시뮬레이션을 회고해
본다.
그냥 회고해 보면 약간 심심하니 R의 ggplot2 와 gganimate 패키지를 학습할 겸 곁들여 시뮬레이션을 생동감있게 해보고자 한다.
Newton Raphson method
Newton Raphson method 는 평균값 정리(mean value theorem) 혹은 테일러 근사(taylor approximation)를 근간으로 근사치를 반복하여 업데이트 하는 개념을 이용한다.
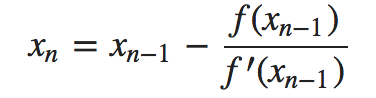
여기서 xn 의 n을 계속
증가시켜 가다 보면 수렴하게 되는데 x∞ 을 f(x) = 0 의 해로
판단한다.
단 무한대로 반복할 순 없기 때문에 정지조건을 부여한다.
이 Newton Raphson method 를 구현한 R code 는 아래와 같다.
Newton Raphson Method in R 글을 참조함
newton <- function(fun, tol = 1e-7, x0 = 1, N = 300){
h <- 1e-7
i <- 1
x1 <- x0
p <- numeric(N)
while(i <= N){
df.dx <- (fun(x0 + h) - fun(x0)) / h
x1 <- (x0 - (fun(x0) / df.dx))
p[i] <- x1
i = i+1
if(abs(x1 - x0) < tol) break
x0 = x1
}
return(p[1:(i - 1)])
}정의된 newton() 함수를 이용해 f(x) = x3 + 2
함수의 f(x) = 0 의
해를 초기값 2 에서 찾기 시작하면
fun <- function(x) x^3+2
newton(fun, x0 = 2)## [1] 1.166667 0.287982 -7.846566 -5.241872 -3.518844 -2.399736 -1.715590
## [8] -1.370234 -1.268564 -1.259980 -1.259921 -1.259921이렇게 된다.
tol 값 보다 현시차와 이전시차값의 절대값 차이가 적을 때
정지조건에 의해서 멈추는데
멈추고 나서의 마지막 값이 -1.259921 이며 Newton Raphson
method 는 이 값을 x3 + 2 = 0 의 해로
계산한다.
ggplot2 로 y = x3 + 2 함수의 그래프를 그린 후 이터레이션 별로 어디에 수렴해 가는지 시각화 해보면 아래와 같다.
p <- ggplot(data.frame(x = c(-2, 2)), aes(x = x)) +
stat_function(fun = fun, color = "blue") +
geom_hline(yintercept = 0) +
geom_vline(xintercept = 0)
d <- data.frame(label = 1:length(newton(fun, x0 = 2)),
x = newton(fun, x0 = 2),
y = fun(newton(fun, x0 = 2)))
p2 <- p + geom_point(data = d, aes(x = x, y = y, frame = label)) +
geom_text(data = d, aes(x = x, y = y + 20, label = label, frame = label), size = 3)
p2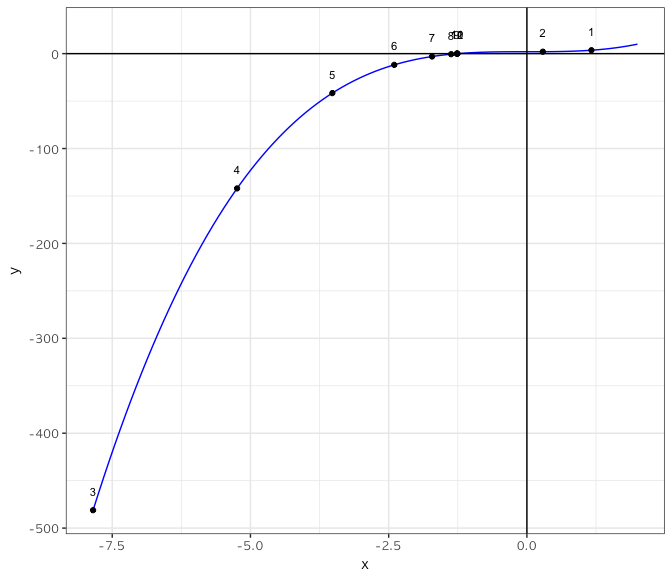
총 12번의 반복을 통해 x = − 1.259921 에 가까워 지는것을 볼 수 있다.
ggplot2 에 gganimate 패키지 조합하여 시뮬레이션 시각화 하기
(개발단계로써 CRAN 에 등록되지 않은) gganimate package는
ggplot2 결과물을 프레임별로 만들어 에니메이션 그림파일을 만들어주는
재미있는 R package 이다.
ggplot2 문법규칙을 그대로 이용하는데 에스테틱에 frame
인자를 지정하기만 하면 된다.
gganimate package 설치는 install_github() 를
이용한다.
devtools::install_github("dgrtwo/gganimate")
library(gganimate)그리고 위에서 시각화한 p2 를 재활용 한다.
gganimate() 함수에 우선 입력해 보면
gganimate(p2)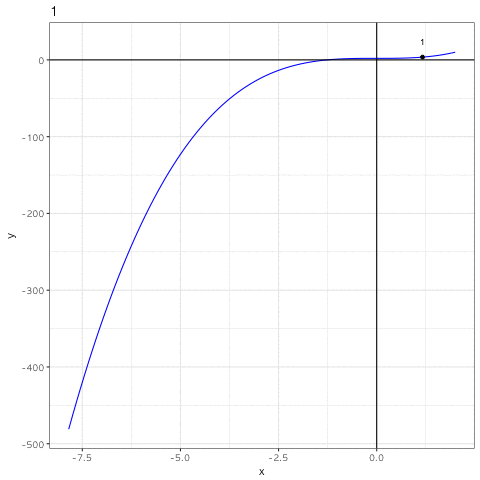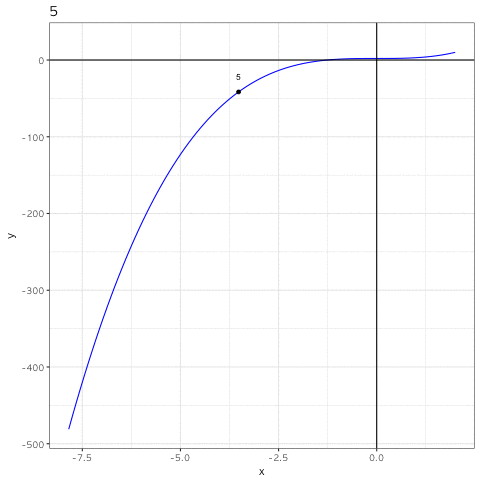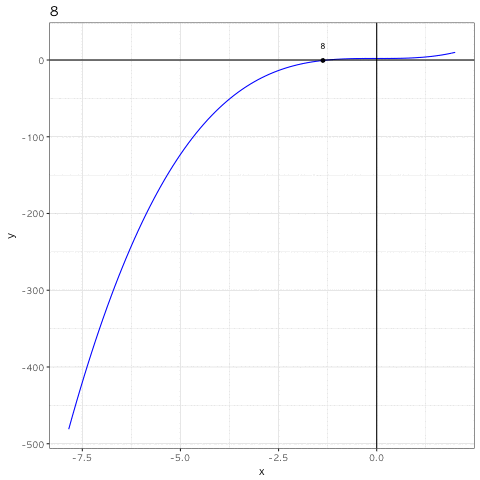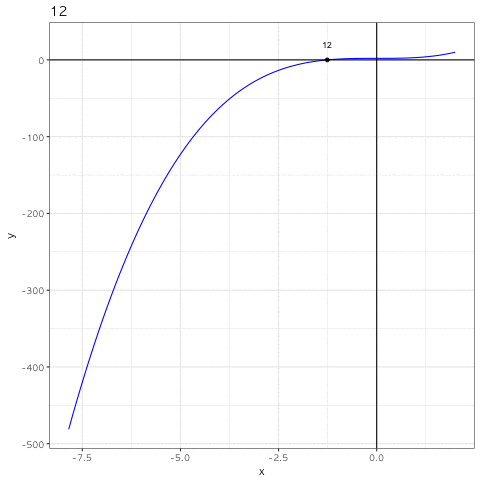
애니메이션 gif 가 잘 출력되는데 p2 에 실은 frame
에스테틱을 미리 선언했기 때문이다.
입력될 ggplot 객체에 frame 에스테틱이 없을 경우
gganimate(p2) 은 에러를 내며 수행되지 않는다.
Error in gganimate(p2) :
No frame aesthetic found; cannot create animation?gganimate() 를 실행해 다양한 옵션과 예제코드를 살펴보면
좋을 것이다.
gganimate package 에는 saveVideo(), saveGIF()
함수가 gganimate() 함수에 연루되어 있으며,
비디오 파일을 만들거나 에니메이션 gif 파일을 만들 때 ffmpeg 를 이용한 다양한
옵션들을 부여할 수 있음을 확인할 수 있을것이다.