일반적인 선형회귀분석보다 모델의 해석이 특수하나
한눈에 이해할 수 있는 모델링 방법인 Step function 을 R에서 구현해보고자
한다.
data(College, package = "ISLR")예제로 사용할 데이터는 ISLR 패키지에 내장되어있는
College 데이터이다.
미국의 여러 대학교가 관측치이고, 각 대학들의 지원자 수와 각 대학들의
정보를 변수로 가지고 있는 데이터셋이다.
summary(College)## Private Apps Accept Enroll Top10perc
## No :212 Min. : 81 Min. : 72 Min. : 35 Min. : 1.00
## Yes:565 1st Qu.: 776 1st Qu.: 604 1st Qu.: 242 1st Qu.:15.00
## Median : 1558 Median : 1110 Median : 434 Median :23.00
## Mean : 3002 Mean : 2019 Mean : 780 Mean :27.56
## 3rd Qu.: 3624 3rd Qu.: 2424 3rd Qu.: 902 3rd Qu.:35.00
## Max. :48094 Max. :26330 Max. :6392 Max. :96.00
## Top25perc F.Undergrad P.Undergrad Outstate
## Min. : 9.0 Min. : 139 Min. : 1.0 Min. : 2340
## 1st Qu.: 41.0 1st Qu.: 992 1st Qu.: 95.0 1st Qu.: 7320
## Median : 54.0 Median : 1707 Median : 353.0 Median : 9990
## Mean : 55.8 Mean : 3700 Mean : 855.3 Mean :10441
## 3rd Qu.: 69.0 3rd Qu.: 4005 3rd Qu.: 967.0 3rd Qu.:12925
## Max. :100.0 Max. :31643 Max. :21836.0 Max. :21700
## Room.Board Books Personal PhD
## Min. :1780 Min. : 96.0 Min. : 250 Min. : 8.00
## 1st Qu.:3597 1st Qu.: 470.0 1st Qu.: 850 1st Qu.: 62.00
## Median :4200 Median : 500.0 Median :1200 Median : 75.00
## Mean :4358 Mean : 549.4 Mean :1341 Mean : 72.66
## 3rd Qu.:5050 3rd Qu.: 600.0 3rd Qu.:1700 3rd Qu.: 85.00
## Max. :8124 Max. :2340.0 Max. :6800 Max. :103.00
## Terminal S.F.Ratio perc.alumni Expend
## Min. : 24.0 Min. : 2.50 Min. : 0.00 Min. : 3186
## 1st Qu.: 71.0 1st Qu.:11.50 1st Qu.:13.00 1st Qu.: 6751
## Median : 82.0 Median :13.60 Median :21.00 Median : 8377
## Mean : 79.7 Mean :14.09 Mean :22.74 Mean : 9660
## 3rd Qu.: 92.0 3rd Qu.:16.50 3rd Qu.:31.00 3rd Qu.:10830
## Max. :100.0 Max. :39.80 Max. :64.00 Max. :56233
## Grad.Rate
## Min. : 10.00
## 1st Qu.: 53.00
## Median : 65.00
## Mean : 65.46
## 3rd Qu.: 78.00
## Max. :118.0018개 만큼의 변수들을 가지고 있는데, 현 분석과정에선 지원서 등록횟수인
Apps 을 종속변수로 하고, 졸업률인 Grad.Rate 를
독립변수로 제한시켜 두 개의 변수만 신경쓰도록 하겠다.
Simple regression model
일반적인 단순선형회귀적합을 하게되면 아래와 같이 모델적합이 된다.
regFit <- lm(Apps ~ Grad.Rate, data = College)
summary(regFit)##
## Call:
## lm(formula = Apps ~ Grad.Rate, data = College)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3764 -2123 -1473 650 44711
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 837.136 541.788 1.545 0.123
## Grad.Rate 33.064 8.006 4.130 4.02e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3831 on 775 degrees of freedom
## Multiple R-squared: 0.02154, Adjusted R-squared: 0.02027
## F-statistic: 17.06 on 1 and 775 DF, p-value: 4.019e-05회귀적합된 1차 선형방정식을 살펴보면
Apps = 837.14 + 33.06 × Grad.Rate
졸업률이 한 단위 증가하면 지원자 수도 33.06회만큼 증가하는 경향을
가진 것으로 알 수 있다.
실제 데이터의 산포와 산출된 회귀적합선을 겹쳐 표현하면 아래와 같다.
plot(Apps ~ Grad.Rate, data = College, col = "grey", pch = 21)
lines(sort(College$Grad.Rate), sort(predict(regFit)), col = "blue", lwd = 2)
grid()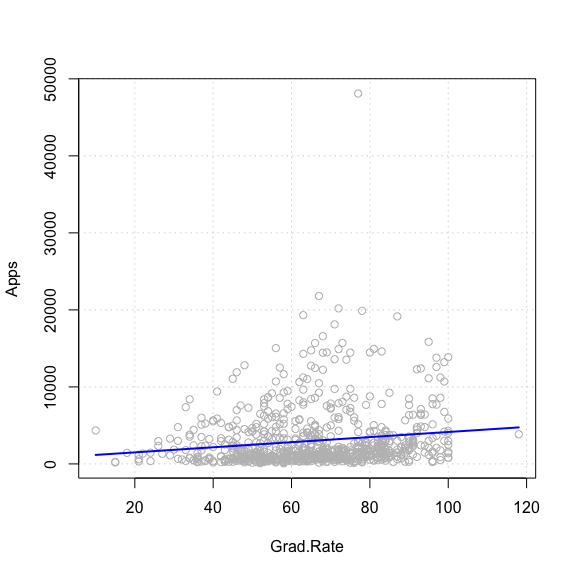
분명 학교의 졸업률이 높으면 높을수록 대학교의 인기가 높은
것인지
해당학교의 지원자가 많아지는 경향을 그림을 보면 알 수 있다.
Grad.Rate 의 회귀계수 또한 베타계수가 0이라는 귀무가설을
기각시키는 P-value 이다.
Step function model
자 그러면 이제 언급할 Step function model 은 위의 일반적인 선형회귀적합과 어떤 차이가 있을까?
stepFit <- lm(Apps ~ cut(Grad.Rate, 2), data = College)
summary(stepFit)##
## Call:
## lm(formula = Apps ~ cut(Grad.Rate, 2), data = College)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3322 -2115 -1483 681 44631
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2494.0 199.7 12.486 < 2e-16 ***
## cut(Grad.Rate, 2)(64,118] 969.1 276.0 3.511 0.000471 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3842 on 775 degrees of freedom
## Multiple R-squared: 0.01566, Adjusted R-squared: 0.01439
## F-statistic: 12.33 on 1 and 775 DF, p-value: 0.0004714lm() 함수의 formula 인자부분의 독립변수에 해당되는
부분을 보면 cut(Grad.Rate, 2) 으로 되어있는데 이것의 의미는
Grad.Rate 변수값들을 두 부분으로 범주화(grouping)
시키겠다는 의미이다.
어떻게 범주화를 시키느냐? 한쪽은 값이 낮은 그룹, 나머지 한쪽은 값이 높은
그룹으로 이분류가 자동적으로 된다.
그리고 위에서 출력된 summary(stepFit) 의 결과물을 이용해
종속변수 Apps 의 모델 방정식을 표현하면 아래와 같다.
Apps = 2494.0 + 969.1 × cut(Grad.Rate,2)(64, 118]
단 위에서 cut(Grad.Rate,2)(64, 118]
의 값은 Grad.Rate 값이 64 < Grad.Rate ≤ 118
일 때 1, 아니면 0의 의미이다.
실제 데이터 산포와 stepFit 적합선을 겹처 그려보면
plot(Apps ~ Grad.Rate, data = College, col = "grey", pch = 21)
lines(sort(College$Grad.Rate), sort(predict(stepFit)), col = "blue", lwd = 2)
grid()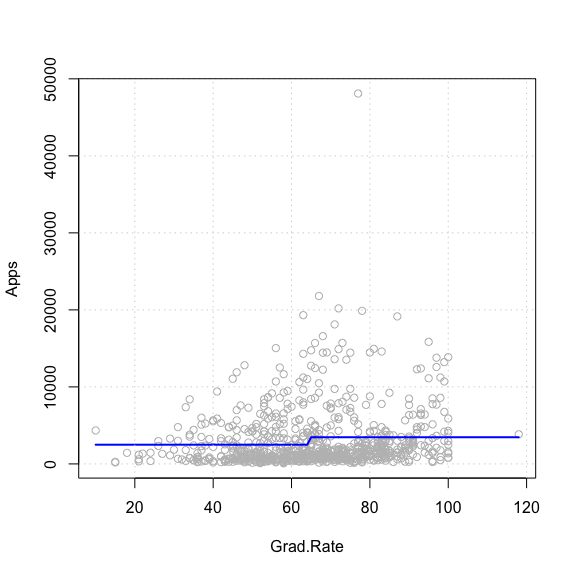
Grad.Rate 의 값이 낮은 그룹, 즉 졸업률이 64% 이하인
그룹은 2493.99회로, 64% 이상인 그룹은 3463.13회로 예측이 되는 모델인
것이다.
이처럼 모델의 형태가 계단(Step)의 형태로 적합 시키며 독립변수의 구간을 계단처럼 구분지은후 각 그룹구간별 종속변수의 값을 예측하게 되는 특성을 가진다.
step function model 을 구현하기 위한 방법은 위의 예제처럼 R에서
cut() 함수를 통해 간단히 구현할 수 있다.
lm() 함수를 이용한 적합은 그대로 두고, formula 인자부분만
알맞게 조정하면 되는데
범주화를 시키고자 하는 독립변수에 cut() 함수를 씌우고
범주화 개수를 지정시키면 된다. (더 특수하게 범주화시키고자 한다면
cut() 함수의 도움말을 이용해 응용해 볼 수도 있겠다)
Example step function model
2개가 아닌 3개의 그룹으로 나누어 step function 적합한 경우의 코드 및
결과이다.
덧붙이면 update() 함수를 통해 이전 객체
stepFit 을 재활용 하고, 형식만 변형했다.
stepFit3 <- update(stepFit, Apps ~ cut(Grad.Rate, 3))
plot(Apps ~ Grad.Rate, data = College, col = "grey", pch = 21)
lines(sort(College$Grad.Rate), sort(predict(stepFit3)), col="blue", lwd = 2)
grid()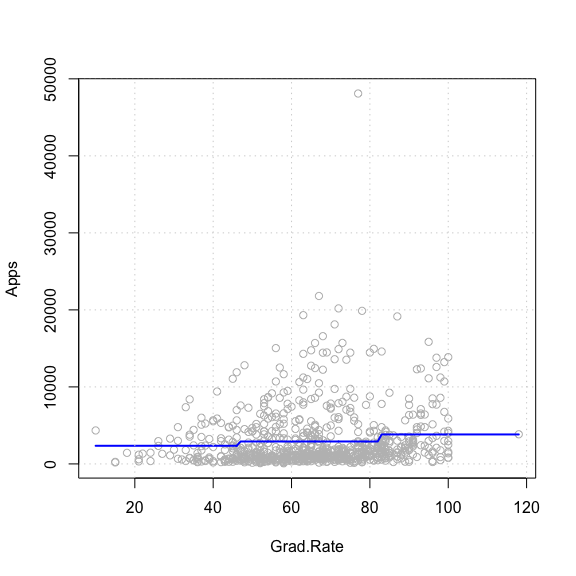
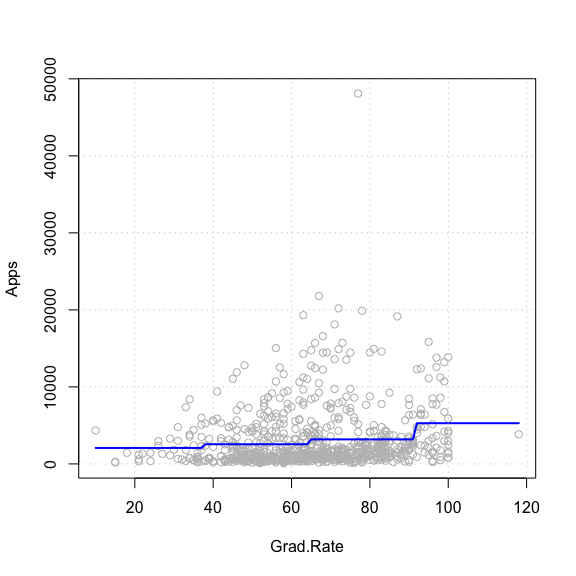
이번엔 4개로 해보면?
다음과 같다.
stepFit4 <- update(stepFit, Apps ~ cut(Grad.Rate, 4))
plot(Apps ~ Grad.Rate, data = College, col = "grey", pch = 21)
lines(sort(College$Grad.Rate), sort(predict(stepFit4)), col = "blue", lwd = 2)
grid()