행렬과 행렬간 곱셈은 행렬 A와 B가 아래와 같이 주어졌을 때
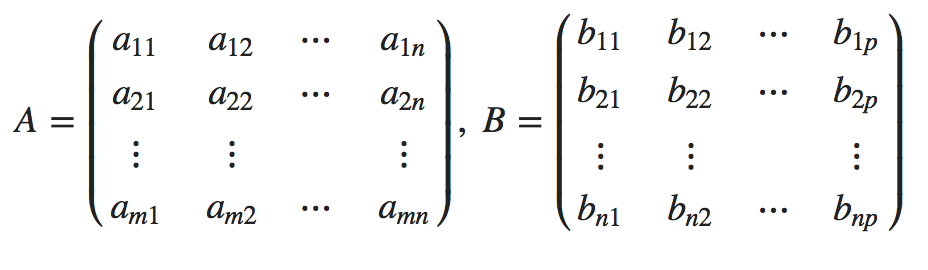
행렬 A와 행렬 B의 곱은
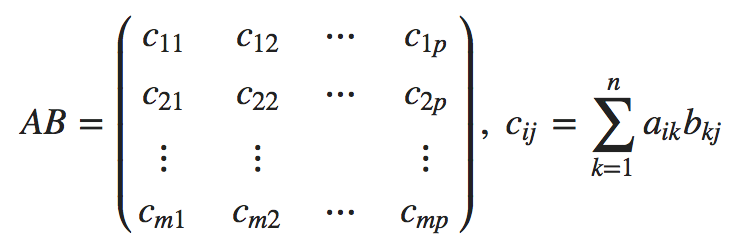
이며, 이때 앞에 위치한 행렬의 열의 수와 뒤에 위치한 행렬의 행의 수가
같아야 행렬곱이 가능하다.
R에서 위와 같은 행렬의 곱셈을 실행하기 위해서는 * 연산자가
아닌 %*% 를 이용한다.
(A <- matrix(c( 2, 7, 1, 3), nrow = 2, ncol = 2))## [,1] [,2]
## [1,] 2 1
## [2,] 7 3(B <- matrix(c(-2, 7, 1, -3), nrow = 2, ncol = 2))## [,1] [,2]
## [1,] -2 1
## [2,] 7 -3A %*% B## [,1] [,2]
## [1,] 3 -1
## [2,] 7 -2일반적인 행렬의 곱셈은 %*% 을 이용해야 한다고
했는데
그럼 * 이것을 이용하면 어떻게 될까?
하다마드 곱셈 (Hadamard Product)
A * B## [,1] [,2]
## [1,] -4 1
## [2,] 49 -9동일한 위치의 원소끼리의 곱이 되어 버린다.
사실 동일차원의 행렬끼리 동일위치원소와 곱해지는 곱셈을 하다마드
곱셈(Hadamard Product) 이라고도 부르는데, 위의 코드가 바로 하다마드
곱셈을 하는 코드로 볼 수 있겠다.
여하튼 R에서는 %*% 사이에 행렬객체를 넣고 실행하면 행렬간
곱셈을,
* 사이에 넣어주면 하다마드 곱셈을 실행킨다는 차이를 확인할
수 있다.
크로네커 곱셈 (Kronecker Product)
행렬의 곱셈 중 크로네커 곱셈(Kronecker Product)이라는 것도
있다.
가끔 요긴하게 쓸 때가 있는 이 크로네커 곱셈은 이런 형태이다.
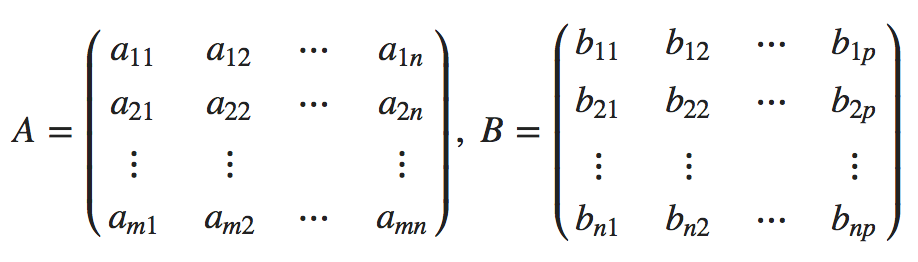
일 때 행렬 A와 행렬 B간 크로네커 곱셈 A ⊗ B 는 아래와 같다.
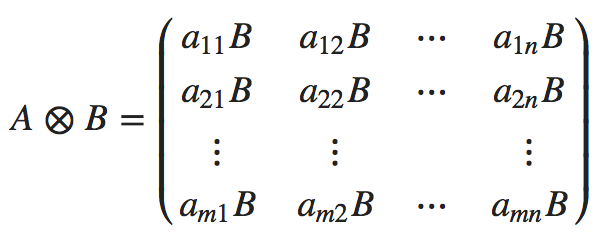
A ⊗ B 를 계산한 후 행렬의 크기를 보게 된다면 mn × np 행렬이 만들어 지게 될 것이다.
크로네커 곱셈을 이용하면 행렬의 크기는 크되 일정한 규칙이 존재하는
행렬을 손쉽게 만들 수 있을 것이다.
예를 들면 아래와 같은 행렬을 R에서 만들어 보겠다고 가정한다.
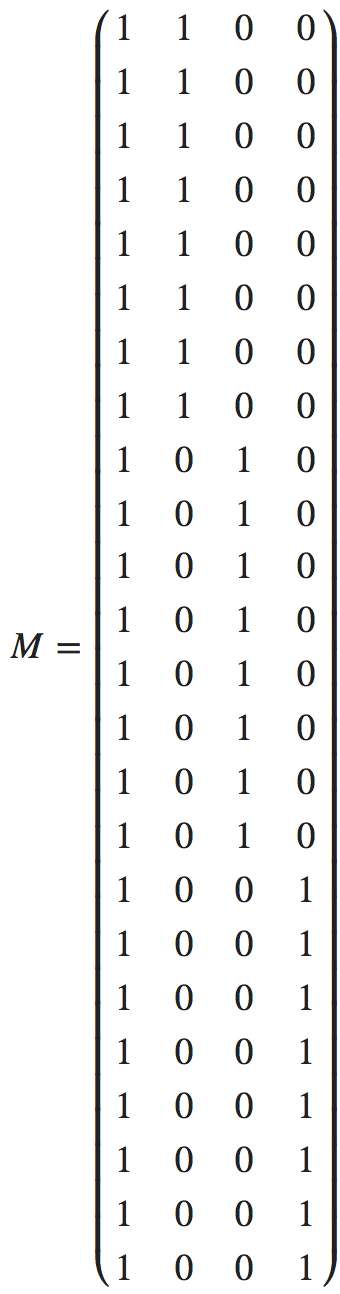
이 행렬 M을 만들기 위해
e <- c(rep(1, 32), rep(0, 24), rep(1, 8), rep(0, 24), rep(1, 8))
(M <- matrix(e, ncol = 4))## [,1] [,2] [,3] [,4]
## [1,] 1 1 0 0
## [2,] 1 1 0 0
## [3,] 1 1 0 0
## [4,] 1 1 0 0
## [5,] 1 1 0 0
## [6,] 1 1 0 0
## [7,] 1 1 0 0
## [8,] 1 1 0 0
## [9,] 1 0 1 0
## [10,] 1 0 1 0
## [11,] 1 0 1 0
## [12,] 1 0 1 0
## [13,] 1 0 1 0
## [14,] 1 0 1 0
## [15,] 1 0 1 0
## [16,] 1 0 1 0
## [17,] 1 0 0 1
## [18,] 1 0 0 1
## [19,] 1 0 0 1
## [20,] 1 0 0 1
## [21,] 1 0 0 1
## [22,] 1 0 0 1
## [23,] 1 0 0 1
## [24,] 1 0 0 1와 같은 형식의 코드를 짤 수도 있다.
하지만
c(rep(1, 32), rep(0, 24), rep(1, 8), rep(0, 24), rep(1, 8))
처럼 손이 많이 가는 코드를 작성해야 하는데, 크로네커 곱셈을 약간
응용하면 행렬 M을 좀 더 편하게 만들 수 있을 것이다.
R에서 크로네커 곱셈을 수행하는 함수는 kronecker() 이다.
(A <- matrix(c(1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1), ncol = 4))## [,1] [,2] [,3] [,4]
## [1,] 1 1 0 0
## [2,] 1 0 1 0
## [3,] 1 0 0 1(B <- matrix(rep(1, 8)))## [,1]
## [1,] 1
## [2,] 1
## [3,] 1
## [4,] 1
## [5,] 1
## [6,] 1
## [7,] 1
## [8,] 1(M <- kronecker(A, B))## [,1] [,2] [,3] [,4]
## [1,] 1 1 0 0
## [2,] 1 1 0 0
## [3,] 1 1 0 0
## [4,] 1 1 0 0
## [5,] 1 1 0 0
## [6,] 1 1 0 0
## [7,] 1 1 0 0
## [8,] 1 1 0 0
## [9,] 1 0 1 0
## [10,] 1 0 1 0
## [11,] 1 0 1 0
## [12,] 1 0 1 0
## [13,] 1 0 1 0
## [14,] 1 0 1 0
## [15,] 1 0 1 0
## [16,] 1 0 1 0
## [17,] 1 0 0 1
## [18,] 1 0 0 1
## [19,] 1 0 0 1
## [20,] 1 0 0 1
## [21,] 1 0 0 1
## [22,] 1 0 0 1
## [23,] 1 0 0 1
## [24,] 1 0 0 1이처럼 kronecker(A, B) 코드를 실행하면 A ⊗ B 를 연산해준다.